直方体の最長経路問題

先日次のような問題と出会ったので紹介します。ちなみに私は吉祥寺で2時間余り，その後も中央線に乗りながら神田まで考えたのですが明快な解答にたどり着けませんでした。

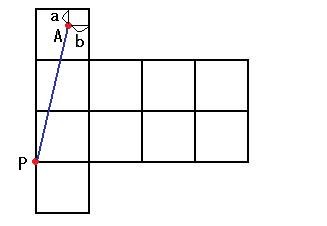
「下図のような辺の長さが1,1,2の直方体の一頂点にアリがいて面上を動き回るとき，アリが到達するのに経路が最長となる点はどこか。ただし点への経路は考えられるものの中で最短のものをとるとする。」

直観だと対頂点（ここではある頂点に対して空間上の対角線で結ばれた頂点とします）のような気がします。実際面上ではなく直方体の内部も経路に含めてよいとするならば，対角線が最長となるので対頂点が最も遠い点となります。また，経験上立方体ならば面上のみの経路でも対頂点が最遠点になることはわかります。

ああでもない，こうでもないと帰納的（頭に"数学的"はつきません）にアプローチしてみると，大体の目星はつけられそうです。具体的には，ヒモかなんか用意して，実際に直方体に巻きつけてみると，対頂点までに必要な長さでは届かない場所があることがわかります。

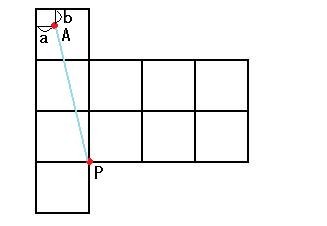
そうすると，アリのたどる経路の始点を点Pとすれば，経路が最長となる点Aは次の図のあたりにあることがわかります。では，具体的にどのような点なのかを求めてみましょうか。点Aを含む面において，その面を構成する辺のうち，点Aから2辺にそれぞれ下図のように垂線を引き，その長さをa,bとします。

次のように経路PAが4通りほど考えられます。合わせて記した経路は，互いに側面の通り方が類似しています（後で考察）。

それぞれについて展開図を用いて経路の長さを求めてみます。三平方の定理を用いてa,bについての文字式になります。

…ア

…イ

…ウ

…エ

これらの等しくなるようなa,bの値を求めれば，点Aの位置が示されます。実質a,bを求めるのに必要な式は3つで足りますが，先ほどの対称性が式にも表れているので，あえて4つとも書きだしてみました。
式（ア）と（イ），（ウ）と（エ）はそれぞれa,bについて対称になっていることがわかります。よってa=bです。まぁa,bのおき方や直方体ということからそれくらい自明だとは思うのですが，式という形で見てみてもそれがちゃんと現われているよ，式での「対称」と図形などにおいての視覚的な「対称」の結びつきがよくわかる例だ，ってことで。
（追記：当初4経路を2組に分けた時点で，「それぞれの組の経路は2線分PQ-QAに関して対称」という旨を書きましたが，これはa=bの場合に言えることでした。当該個所は訂正済。指摘してくれたsilver_sありがとう。）

実際にa,bを求めてみると，a=b=1/4となります。

では，もうちょっと拡張して，1,1,n の直方体だったらどうなるでしょう。n=2の場合をやったので割と容易に類推できると思います。

展開図をもとに，どの部分がnになるのかを考えると，先ほどの式は次のようになります。
ア'：
イ'：
ウ'：
エ'：

この場合でa,bについて解く（nは定数）と，a=b=(n-1)/2nとなります。
先のがn=2の場合でa=b=1/4になるし，立方体の場合はn=1でa=b=0，すなわち点Aは対頂点になります。
ちなみに，nを無限大に飛ばしてみると，a,bは1/2に収束します。したがって，直方体の高さが大きくなるほど点Aは上面の中心に近づいていくことがわかります。

とまぁ自分の頭の整理も兼ねて久々にここに書いてみました。最後にこの問題に関しての課題と展望を付しておきます。「点Aが上面にあることの論理的な証明」「点Pを固定しない場合，2点間の経路が最長となるのはどのようなときか」「縦横比も変化させた場合」

最後にこの問題と解説をくれたsilver_sに感謝。